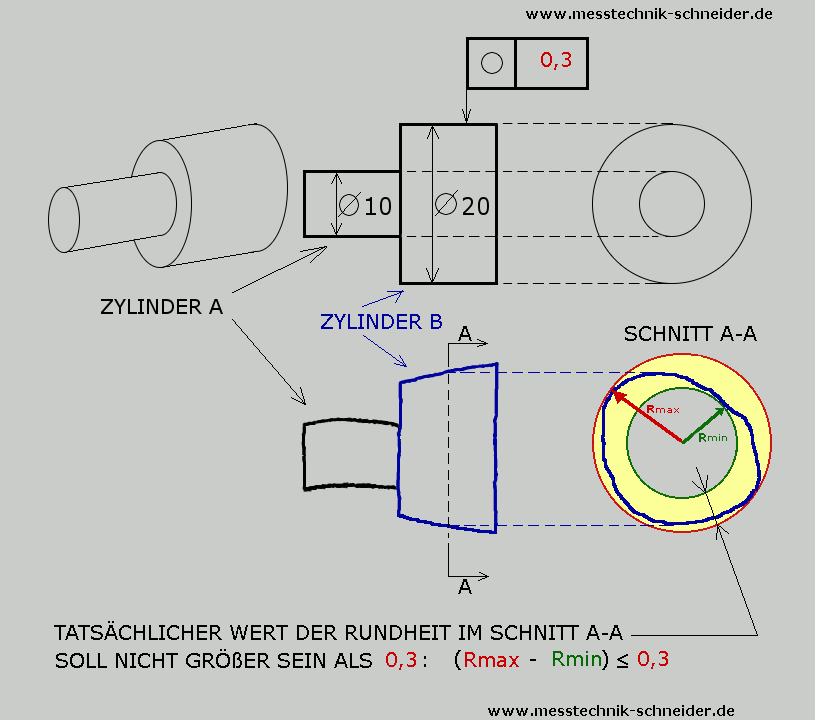
1) Rundheit des Zylinders B in jedem Schnitt soll kleiner sein als angegeben (im Beispiel: <0,3)
2) Das gemeinsame Zentrum von Kreisen der Definition (gebildet nach Tschebischew-minimum-Kriterium)
stimmt normalerweise nicht überein mit dem Zentrum des Istkreises (gebildet nach Gaus).
3) Toleranzpfeil sollte immer senkrecht zur Achse des Elements und entfernt vom Maßpfeil
auf der Zeichnung eingetragen werden.
4) Man stellt sich vor zwei Kreise in einer Schnittebene (senkrecht zur Istachse des Elementes).
Ein Kreis ist komplett im Material. Der andere Kreis ist komplett außen. Die geschnittene Außenkontur des Elementes
befindet sich zwischen beiden Kreisen. Beide Kreise sind fest mit einander gebunden durch das gemeinsame Zentrum.
Die Position dieses Zentrums in der Schnittebene ist frei. Durchmesserwerte von beiden Kreisen sind auch frei.
Und so versucht man in der Schnittebene solche Position von beiden Kreisen zu finden, dass die Breite des Ringes
zwischen beiden Kreisen minimal wird. Die Istkontur wird "festgeklemmt" zwischen beiden Kreisen.
Die oben beschriebene Vorgehensweise veranschaulicht die so genannte Minimumbedingung,
die mathematisch als "Tschebyschew-Kriterium" definiert wird.
5) Unterschied zum Rundlauf:
Bei der Prüfung des Rundlaufs liegt das Zentrum von beiden Kreisen auf der Bezugsachse (ist an sie festgebunden).
Bei der Rundheit dagegen gibt es keinen Bezug.
Zwei Kreise können in der Schnittebene frei bewegt werden bei der Suche des minimalen Abstandes zwischen ihnen.
Deshalb ist die Rundheit in einem Schnitt normalerweise kleiner als der Rundlauf.
HIER ZUR DEFINITION DES RUNDLAUFS