Koaxialität eines Zylinders (im Beispiel: Zylinder B) zu einem Bezugszylinder (im Beispiel: Zylinder A),

   ist gleich dem verdoppelten Wert des Abstandes (im Beispiel: Amax) vom maximal entfernten

   Punkt der Istachse des Zylinders (B) bis zur Bezugsachse des Bezugszylinders (A).

   Diese tatsächliche Koaxialität soll kleiner sein als auf der Zeichnung angegeben ist:

   Im Beispiel: (Koax = 2 x Amax) < 0,3

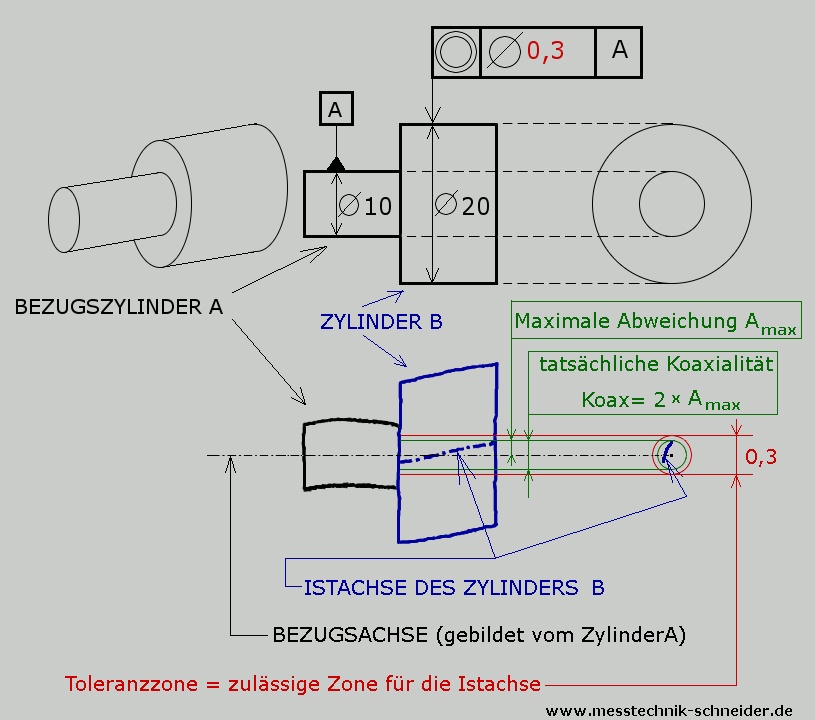
   1) Bezugsachse wird gebildet nach den Regeln für Bezugsbildung.

   2) Istachse wird so gebildet: Einzelne Kreise erfassen auf der ganzen Länge des Zylinders B.

   Diese Kreise befinden sich in den Ebenen, die senkrecht zur Bezugsachse sind.

   Zentren von diesen Kreisen bilden die Istachse. Je mehr Kreise gebildet werden, desto genauer

   wird die Istachse bestimmt. Kreise werden nach Gauss gebildet. Je mehr Punkte für einen Kreis angetastet werden,

   desto genauer wird das Zentrum des Kreises bestimmt.

   3) Toleranzzone: Idealer Zylinder mit dem für die Koaxialität angegebenen Durchmesser (im Beispiel: 0,3).

   Seine Achse ist gleich der Bezugsachse. Alle Punkte der Istachse sollen sich innerhalb von diesem

   Toleranzzylinder befinden.

   4) Wenn die Achse des Zylinders B (oder beide Achsen: vom Zyl. A und vom Zyl. B )

   bis zum Grenzfall (bis zu einem Punkt) verkürzt wird (werden),

   dann spricht man von " Konzentrizität ". Siehe Begriff " Konzentrizität " .