Zum Glossar |
Zur Startseite |
BEGRIFF EBENHEIT: DEFINITION |
|
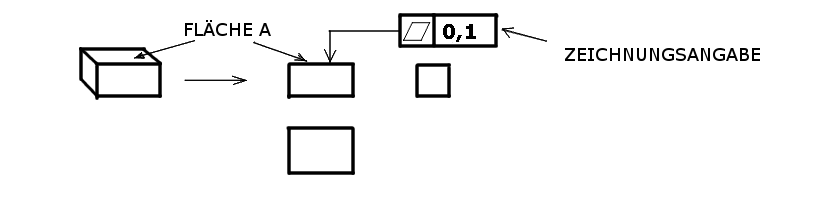
Ebenheit einer Fläche ist gleich dem minimalen Abstand zwischen zwei idealen Ebenen, |

|
|
|
|
BEDEUTUNG / BEGRIFFSERKLÄRUNG |
|
|
|
|
Kommentar: |
|
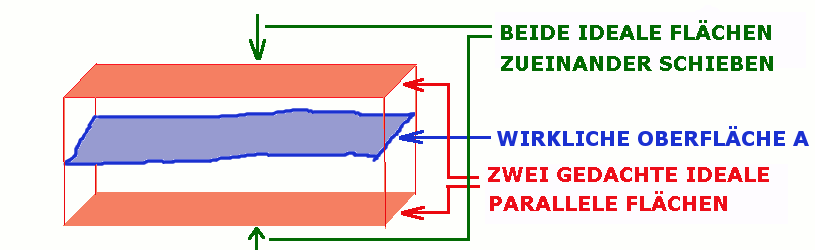
Zwei ideale parallele Flächen so zueinander bis zum Anschlag schieben, dass der Abstand zwischen beiden idealen Flächen minimal wird. Dabei: 1) Wirkliche Fläche A wird zwischen beiden idealen Flächen "zusammen gepresst", " darf " aber nicht verformt werden. Normalerweise entstehen dabei vier Berührungspunkte. zum Beispiel: Drei mit der unteren idealen Fläche und ein Punkt mit der Oberen. 2) Beide ideale Flächen bleiben immer parallel und dürfen im Raum beliebig gedreht und geschoben werden, so dass der minimale Abstand zwischen beiden idealen Flächen erreicht wird. Die oben beschriebene Vorgehensweise veranschaulicht die so genannte Minimumbedingung, die mathematisch als "Tschebyschew-Kriterium" definiert wird. Der auf solche Weise gefundene minimale Abstand zwischen beiden idealen Flächen ergibt den tatsächlichen Wert der Ebenheit der wirklichen Oberfläche A. Er muss dann nicht größer sein als auf der Zeichnung angegeben. Im Beispiel oben: Nicht größer als 0,1 mm. |
bei Wikipedia
|
Zum Glossar |
Zur Startseite |